Золотое сечение или золотая пропорция известна тысячи лет, её применяли ещё в Античной Греции. Это природная закономерность, природная пропорция, можно называть как угодно, но она встречается в природе и окружает нас. Она для нас очень привычна, хотя мы это и не отслеживаем, но наш мозг считывает её как паттерн и воспринимает как что-то хорошее и красивое.
Золотая пропорция — это пропорция асимметрии, но соотношение частей такое, что создает гармонию и выглядит эстетично, что подразумевает для нас «выглядит привычно», «выглядит естественно». Золотая пропорция имеет идеальное соотношение частей, когда отношение меньшей части к большей такое же, как большей части к целому. Это динамическая симметрия и она характерна для роста живой материи.
Я уже писала о золотой пропорции в статье про восприятия человеком красоты, и приводила исследования генетиков и там же рассказывала о том, что все красивые лица на взгляд человека вписываются в пропорцию золотого сечения. Эта тема будоражила деятелей творчества очень много веков. Архитекторы, скульпторы и художники пытались внедрить в свои творения эти пропорции, чтоб достичь красоты. Сегодня происходит все то же самое, и дизайнеры создают свои продукты с учетом этой пропорции.
Давайте разбираться, что такое Золотое сечение
Если опустить всю сложную терминологию и упростить до процентных соотношений, то золотая пропорция будет такой: 100%=62%+38%
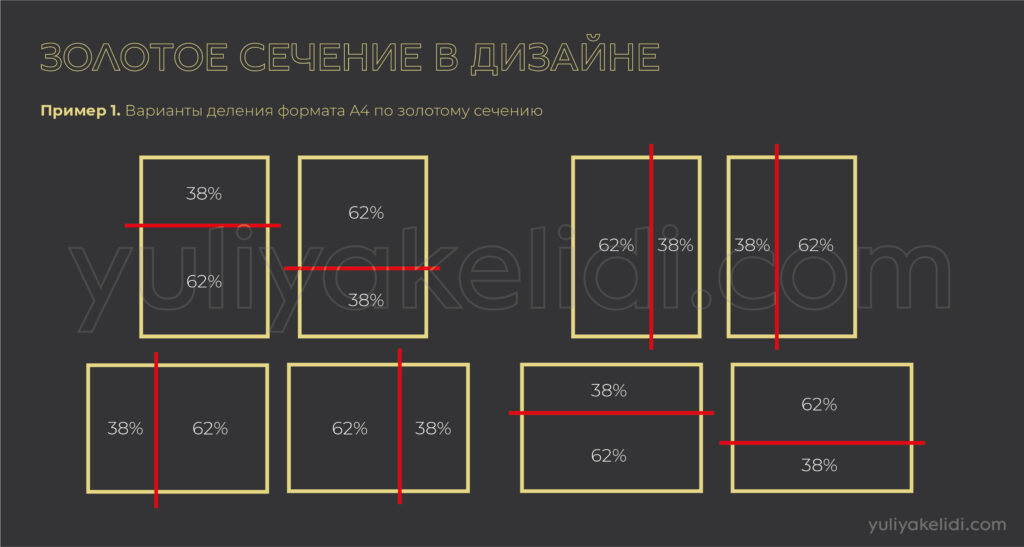
Проще говоря, золотая пропорция это деление объекта на две неравные части, где одна часть занимает 62% от целого, а вторая часть занимает 38% от целого.
И получается, что 62% относится к 100%, точно так же как 38% относится к 62%. Отсюда любой объект можно делить бесконечно.
Пример 1. Всё что угодно, целое, мы берём за 100%. Например, формат A4, т.е. вся его площадь это у нас 100%. Чтоб его поделить пополам по золотому сечению мы делим на неравные части, где одна часть занимает 62%, а другая 38%. Все.
Пример 2. У нас есть дорога. Она длиной 2000 м. её надо поделить по золотому сечению. Мы находим, сколько будет 62% от 2000 м. Получается 1240 м. Мы делим нашу дорогу 2000 м. на отметке в 1240 м. И получим деление прямой по золотой пропорции. Все.
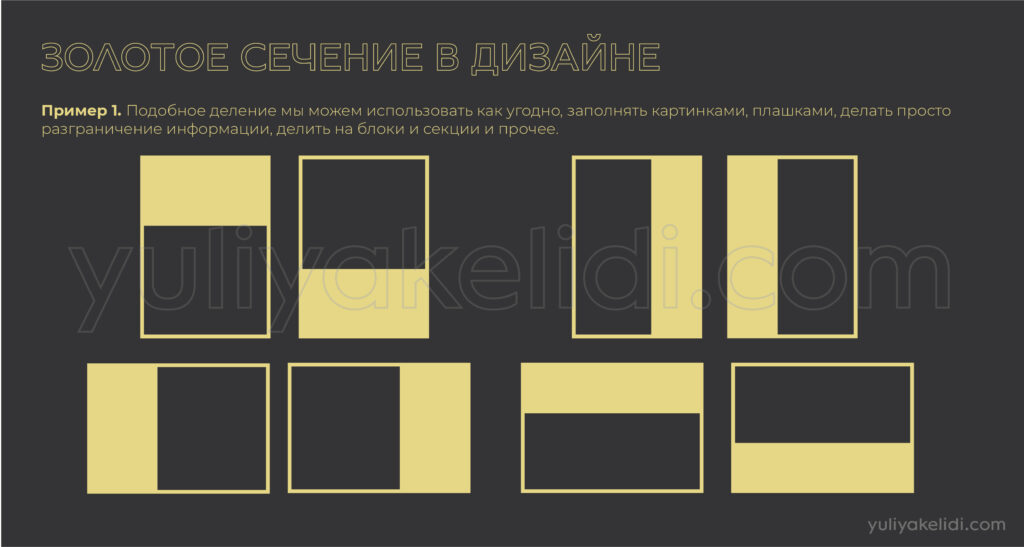
Пример 3. Нам надо чтоб общий объем объектов был расположен к целому по золотой пропорции. Например, в плакате мы хотим, чтоб информация была распределена по золотому сечению.
Шаг 1. Формат плаката это наши 100%. Весь текст и картинки мы собираем вместе и они должны занять площадь на плакате в 62%. Остальное будет воздухом.
Шаг 2. Мы в этом объеме 62% подбираем оптимальные размеры для каждого объекта и потом распределяем по плакату.
Итого: наши объекты суммарно займут 62% площади плаката, а 38% площади плаката останется в качестве свободного пространства, т.е. воздуха. Все.
Пример 4. Нам нужно задать ритмический ряд, который будет уменьшаться в золотой пропорции. У нас есть условный объект. Его изначально мы задаем в размерах, допустим 50 мм, которые обозначаем как 100%. Следующая копия этого объекта должна быть 62%, т.е. от 50 мм. мы находим 62%. Это будет 31 мм. Далее, чтоб найти размер следующего объекта, мы берем 31 мм как 100% и от него находим 62%. Получается 19,22. Следующий будет 11,9 мм. Все.
Пример 5. Например, используя золотое сечение, мы можем найти идеальные значения кегля шрифта. Самый крупный текстовый блок у нас идёт 120 pt, чтоб найти размер кегля для меньшего текста, но с золотой пропорцией, мы задаём его в размере 62% от 120. Получаем 74 pt, следующий блок мы уже ищем 62% от 74. Получаем 46 pt. Это и будет уменьшение кегля текста с учетом золотого сечения.
Вариантов применения очень и очень много!
Идеальный прямоугольник по золотому сечению
Чтоб получить знаменитый золотой прямоугольник, по которому потом строится самая знаменитая кривая, нам надо также построить его в пропорциях 62%-38%.
Одна сторона прямоугольника будет равна 62%, а вторая 38%. В сумме они дают 100%. Получается та самая, знаменитая формула, которую записывают в обозначениях a,b,c.
Как звучит определение золотого сечения:
Золотая пропорция — соотношение двух величин, при котором большая величина относится к меньшей, так же, как сумма величин к большей. И далее невероятно сложное объяснение с кучей формул. Давайте упрощать и разбираться, что это все значит. Потому что дизайнеру, для работы, все эти формулы не нужны.
Итак,
100% — это с,
38% — это а,
62% — это b
Золотая пропорция гласит, что a:b = b:c. В цифрах мы получаем следующее: 38:62 равняется 62:100. Да, действительно, если мы поделим 38 на 62, то получим 0,62, и если мы 62 поделим на 100, то получим также 0,62.
Золотая пропорция продолжается и гласит, что c:b = b:a. Давайте снова в цифрах: 100:62 и 62:38. И в одном и во втором случае мы получаем 1,61.
Вот цифра 1,61 это число Фибоначчи, это число золотой пропорции, число золотого сечения, называйте, как хотите, это одно и то же. По-гречески называют «фи» —φ. Его округляют до 1,62. Что в целом и означает 62% от 100%.
И получается пропорция, которую записывают как соотношение 62%-38%!
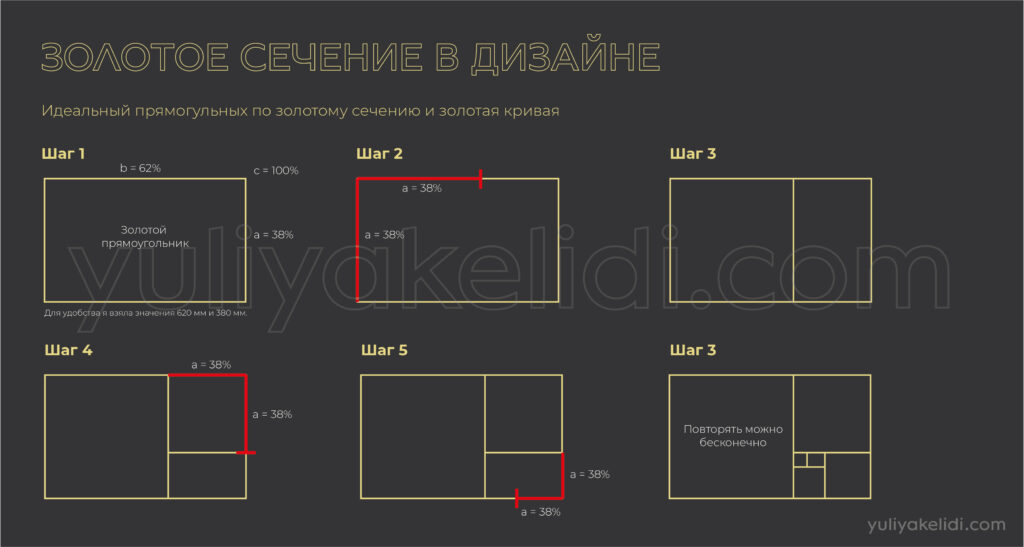
У золотого прямоугольника короткая сторона а — 38%, а длинная b — 62%. Для удобства, давайте и зададим числа 38 мм и 62 мм. Получим золотой прямоугольник.
Сторону b мы берем как 100 и делим её на 62% и 38%. К слову 62% от стороны b будут равняться 38 мм, т.е. стороне а. Таким образом мы получаем квадрат.
Дальше каждую сторону мы делим на пропорцию 62 и 38 и наш прямоугольник будет уменьшаться до бесконечности.
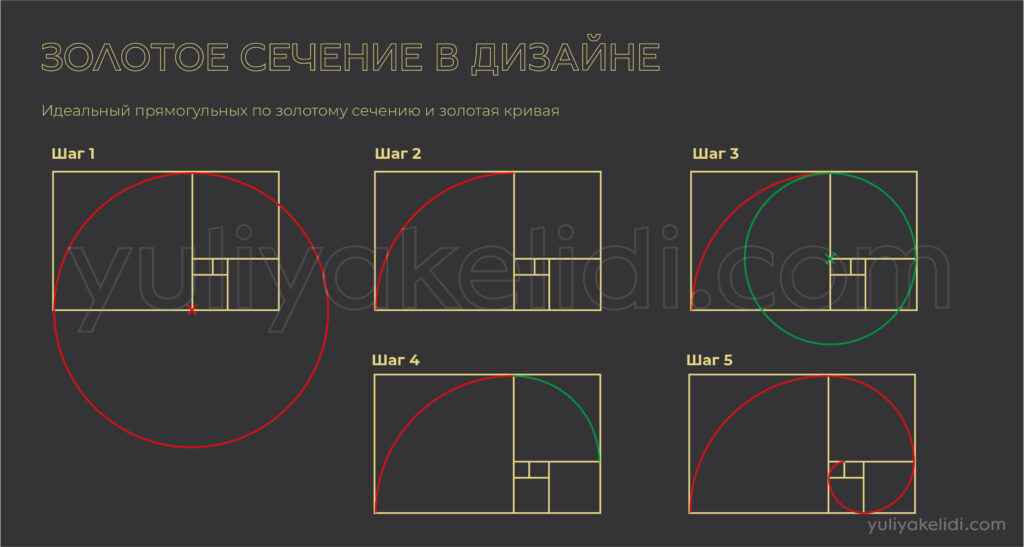
В получившиеся квадраты мы вписываем окружность. И соединяясь, она рисует нам природную кривую, которая характерна для живой материи.
Вот и всё)
И ещё.
В 2023 году я решила создать youtube-канал, на котором буду размещать обучающие ролики по графическому дизайну, также будут ролики про искусство.
Начала я записывать с уроков по изучению программы Adobe Illustrator.
Если вам интересно то, что я делаю, вы можете поддержать меня. Вот ссылка на канал, подпишитесь, пожалуйста.
Также мне важна любая обратная связь, чтоб создавать материалы ещё качественнее.
Теперь у меня появилась страница на Facebook. Если вам интересна эта тема, можете присоединиться и следить за выходом новых статей. Буду рада вас видеть 🙂